Problem #111
Tags: depth first search, start and finish times
Suppose a depth-first search (DFS) is run on the graph shown below using node \(s\) as the source and adopting the convention that a node's neighbors are produced in ascending order of their label.
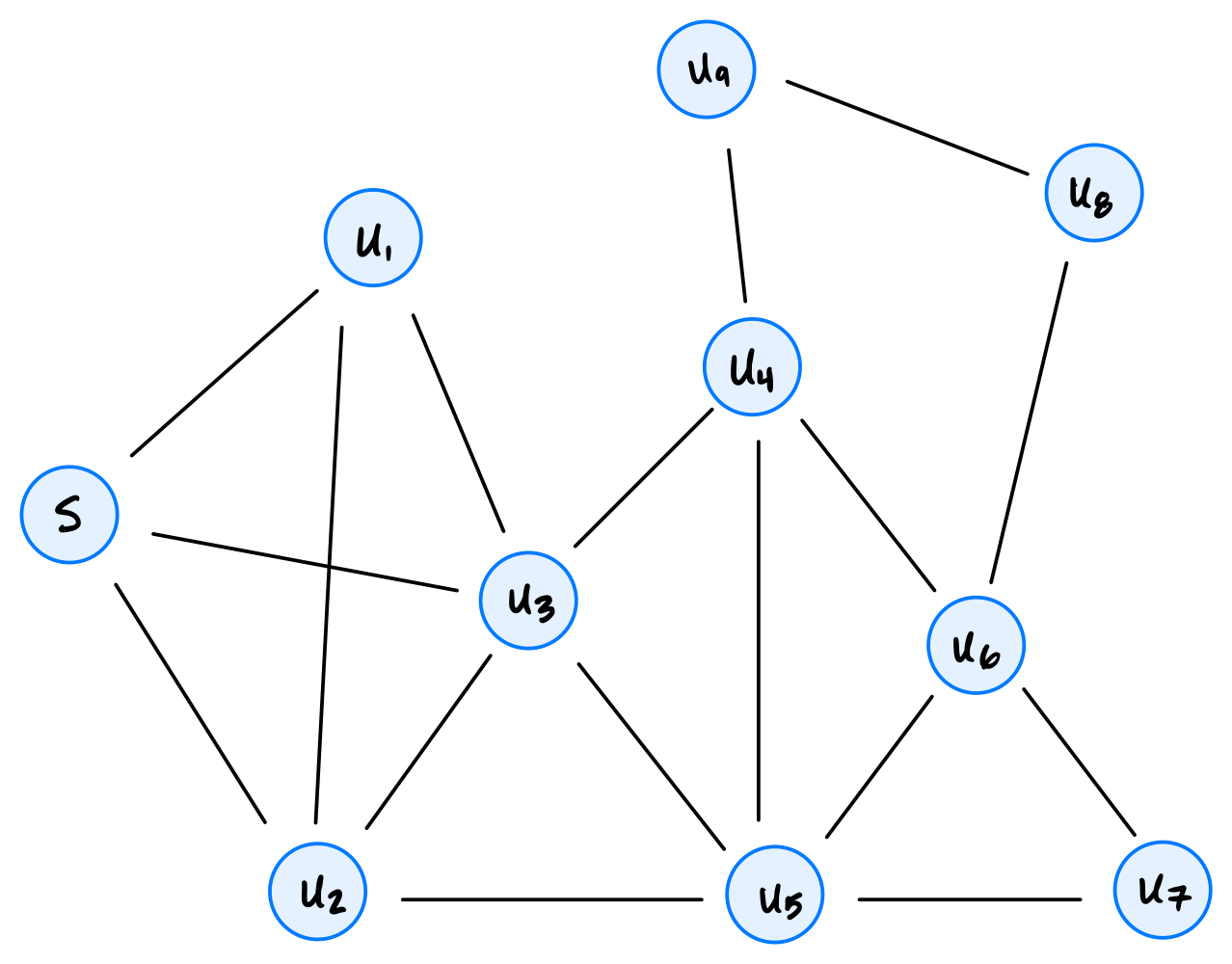
Part 1)
What will be the start time of node \(u_7\)?
Solution
8
Part 2)
What will be the finish time of node \(u_7\)?
Solution
9
Part 3)
Which node will be the DFS predecessor of node \(u_7\)?
Solution
\(u_6\)